Constantino Tsallis, que encontrou na beleza dos fractais no início da década de 1980 a sua inspiração para formular a teoria da q-Statistics, é eleito para a Academia Europeia de Ciências e Artes, que inclui, dentre seus membros, 38 Prêmios Nobel em todas as áreas.
Em meio ao vento frio numa praça circular no Instituto de Física da Universidade de São Paulo (IFUSP), Nayra Cristina, 21 anos, tocava viola, instrumento que começou a aprender aos 12 anos de idade. A estudante do terceiro ano de Física, moradora do Conjunto Residencial da USP (Crusp), estudava seu instrumento a poucos passos do Auditório Abrahão de Moraes, onde acontecia, naquele 1º de julho de 2024, o simpósio “Dos Raios Cósmicos aos Aceleradores de Partículas” em homenagem aos cem anos de nascimento do físico César Lattes, 90 anos da USP e 70 anos do CERN, a organização europeia que administra o maior acelerador de partículas do mundo.
“Música tem muito a ver com física e matemática, quando se fala em ritmo. Mas tem um lado bem expressivo que às vezes a gente tem na Física, mas na música aparece de forma diferente”, diz a estudante, que deseja seguir carreira na área de Física da Matéria Condensada. Ela lembrou ainda que Galileu Galilei e Albert Einstein também eram músicos, além de grandes cientistas. “Você medita em quem você é, você medita na vida.”
“Platão já falava que beleza e verdade eram sinônimos”, lembra o físico teórico Constantino Tsallis, que encontrou na beleza dos fractais no início da década de 1980 a sua inspiração para formular a teoria da q-Statistics, também conhecida como q-entropia, ou ainda, a Entropia de Tsallis. Nascido na Grécia, mas radicado no Brasil desde 1975, Tsallis é pesquisador Emérito do Centro Brasileiro de Pesquisas Físicas (CBPF) e foi eleito para a Academia Europeia de Ciências e Artes (EASA) em meados de junho.
Aos 80 anos, completos em novembro, Tsallis também ganhou um artigo científico em sua homenagem. “The Statistics of q-Statistics” foi publicado no periódico Entropy, da MDPI, sendo um dos autores Ernesto P. Borges, do Instituto de Física da Universidade Federal da Bahia. Além de abordar as considerações científicas que fizeram da teoria elaborada por Tsallis um novo paradigma que generaliza a entropia de Boltzmann e Gibbs, o estudo traz um gráfico impressionante.
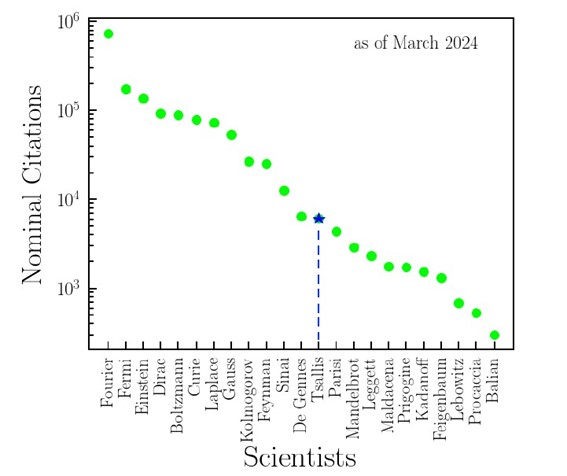
O cientista possui mais de 4 mil citações nominais, que são aquelas em que o nome está no título do artigo ou no seu resumo, até março de 2024, um número muito maior, por exemplo, que o físico italiano Giorgio Parisi, prêmio Nobel de Física em 2021, e o matemático franco-americano Benoît Mandelbrot, conhecido como “o pai do fractais”. “Às vezes, nem eu acredito como é que meu nome aparece com um índice tão alto de citações nominais”, diz Tsallis, em entrevista ao Boletim SBF. “E aí você vê o impacto internacional dessa entropia que, de certa maneira, é um novo paradigma do que que seja o conceito de entropia. É uma mudança de paradigma. E isso tem um impacto muito grande”, diz. Acompanhe trechos da entrevista com Tsallis abaixo:
O senhor pode comentar sobre a fusão de arte e física no seu trabalho, que se dá muito porque o senhor acha bela algumas equações, algumas questões da física?
Eu só posso dizer que eu não sou o primeiro. Platão já falava que beleza e verdade eram sinônimos. E o poeta inglês John Keats também. Ele disse: beleza é verdade, verdade é beleza, é tudo o que sabemos e tudo o que precisamos saber. E outros também. A Emily Dickinson também fala disso. Enfim, é uma ideia que eu diria natural no ser humano associar a verdade à beleza. Não há nenhuma originalidade da minha parte, mas eu uso muito isso. Você mencionou as equações matemáticas, claro, porque eu faço física teórica. Mas não somente na física teórica, na física experimental também. Às vezes, tem um experimento que tem uma grande beleza pela sua elegância, pela sua imaginação da configuração experimental que o cientista abordou. Eu uso muito isso. Quando eu vejo uma equação, imediatamente percebo se ela tem alguma beleza ou não. Tenho um amigo que é indiano, A.K. Rajagopal, o qual viveu a vida toda nos Estados Unidos, em Washington, e trabalhava em laboratórios de pesquisa naval fazendo física teórica. E, mais de uma vez, ele e eu ficávamos brincando com a mesma igualdade, sobre como era mais elegante apresentá-la. E quando você a apresenta de uma maneira, que eu diria, otimizada, ela te faz entender mais, ela te faz penetrar melhor no que ela significa, porque finalmente, em física teórica, uma equação nada mais é do que uma tentativa de descrever a natureza. E a natureza é muito complexa, e descrever algum aspecto dela com uma equação é muita arrogância. Mas você consegue geralmente escrevê-la de uma maneira tal que ela quase fala por si só. Então, eu uso muito essa questão para, antes de analisar detalhadamente um cálculo, para eu ver se creio que seja verdade ou não. Ou, em outras palavras, se vale a pena analisá-lo detalhadamente.
E foi essa percepção que o levou à sua teoria de entropia?
É verdade. Eu tive a ideia dessa entropia em 1985, num evento francês, mexicano e brasileiro no México. Eram três delegações e eu liderava a delegação brasileira. E, num certo momento, todo mundo que estava no evento foi para o coffee break. E eu tinha ficado no auditório vendo o Edouard Brezin, um físico importante da França, conversando no quadro com um estudante mexicano, cujo nome não me lembro. E eu estava a uma certa distância, então eu não podia escutar a conversa deles. Mas Brezin escrevia umas equações no quadro, enquanto conversava com o estudante mexicano. Ele estava explicando ao estudante o que são os multifractais, que é uma generalização do conceito de fractal, que é uma forma geométrica invariante por escala. Você faz um zoom para dentro, um zoom para fora, e você praticamente vê a mesma coisa. Então, o multifractal generaliza o conceito de fractal. E nos multifractais aparecem o tempo todo probabilidades com uma potência. E ele estava explicando isso para o estudante. E eu via as equações dos multifractais, e eu pensei: com isso aí dava para generalizar a famosa entropia de Boltzmann e Gibbs.
E então, eu percebi que usar probabilidades com potências, como a palavra indica, potencializa convenientemente a probabilidade. Então, a probabilidade é um número entre 0 e 1. Vamos pegar o exemplo que seja a probabilidade muito pequena, 0,01. Um número muito pequeno. Mas se você bota em cima dele uma potência menor do que 1, por exemplo, raiz quadrada de 0,01, a raiz quadrada vale 0,1, que é 10 vezes maior do que 0,01. Então, a potência dá mais peso ou menos peso às probabilidades. E eu pensei, com essa ideia, dá para generalizar a famosa entropia de Boltzmann. Então, escrevi de um jeito direto, não deduzi porque é um postulado. Você não deduz um postulado. Escrevi e olhei para ela e achei que era bonita. Então, comecei a trabalhar em cima disso.
Sem falar que o próprio Fractal é uma obra de arte pulsante, viva.
Também, claro. Tanto é que meu artigo de 1988, eu demorei três anos em publicar, porque eu me perguntava para que serve isso. E eu não sabia responder essa pergunta. E três anos depois, em 88, comecei a vislumbrar para que podia servir. E no paper de 88, acho que na primeira frase ou na segunda, eu escrevi “Inspired by multifractals”… Quer dizer, eu declaro que a inspiração veio dos multifractais. Porque você sabe tão bem quanto eu que a ciência sempre se inspira em algo que alguém se inspirou em alguma outra coisa, que alguém se inspirou por sua vez em alguma outra coisa. E isso vira um fractal intelectual. Então, eu me inspirei no conceito dos multifractais, como você disse, tem uma beleza, uma fascinação pulsante. E, a partir daí postulei essa expressão de entropia que colegas gentilmente referem com o meu nome.
E a aplicação da sua teoria serviu tanto à fabricação de porcelanas quanto à psicologia…
Sim, sim, sim. O da porcelana é interessante. Utilizando essa expressão, as consequências dessa entropia, pesquisadores franceses do Institut de Céramique de Limoges, que é onde tem as famosas porcelanas de Limoges, com o azul de Limoges. Utilizando então as consequências dessa entropia, conseguiram fabricar porcelanas muito iguais entre elas, muito semelhantes entre elas. E você sabe que um restaurante é bom, não quando a comida às vezes é boa. Um restaurante é bom quando a comida sempre é boa. Então as cerâmicas de Limoges têm que ser sempre boas. Não podem ser às vezes boas e às vezes mais ou menos. Têm que ser sempre boas para terem o valor, o prestígio e o valor comercial que elas têm. Muitos anos atrás, eu visitei uma fábrica de porcelanas em Limoges com a minha primeira esposa, e perguntei: esses pratos aí quanto valem? Tanto… E aí tinha ao lado um que parecia idêntico. Eu perguntei: e esse outro? O preço era bem maior. Eu digo: e qual é a diferença? Ele disse: se você olha o prato assim, você não vê a diferença. Mas se você empilha 10 pratos de um e 10 pratos do outro, você vai ver que o mais caro é sempre igual e a pilha é perfeita. E o outro prato, a pilha não é perfeita. Então, por isso que eu digo, tem que ser sempre bom. E eles conseguiram isso utilizando a q-Entropia (que fundamenta a q-Statistics, o nome da teoria desenvolvida por Tsallis).
Eu nunca publiquei, nem pretendo publicar, essa entropia, chamando-a de Entropia de Tsallis. Isso é uma gentileza, me honra muito que meus colegas chamem essa entropia com o meu nome. Mas eu nunca escrevo, nunca escrevi “entropia de Tsallis”. Se por aí você encontrar algum texto que tenha essa expressão e que eu seja coautor, pode ter certeza que foi algum dos coautores que escreveu e eu não percebi lendo, porque se eu vejo eu sempre risco, eu chamo non-additive entropy ou q-entropia. Mas a expressão é essa mesma.
Na psicologia, o senhor tem um exemplo de como foi aplicada?
Tem muita coisa na psicologia interessante relacionada com isso, mas o exemplo que estudamos mais detalhadamente foi feito com a minha filha Alexandra, é uma coautoria minha com a minha filha, que é doutora em psicologia e professora. Neste momento é chefe de um departamento de psicologia na UERJ, na Universidade do Estado do Rio de Janeiro. A ideia que tentamos ver, se era verdadeira ou falsa, é que a gente aprende ou memoriza coisas por correlações de longo alcance. Então, como a metáfora, como o nome indica, é um transporte. Metáfora, em grego, significa mudança. Se você pega o piano da sua casa e botar em cima de um caminhão e levar para outra casa, isso é uma mudança, não é? Mudança do piano. Isso em grego se chama metáfora. Então, a metáfora é isso. É uma coisa que existe num âmbito e você a leva em outro âmbito.
Por isso Aristóteles escreveu: metáfora, de todas as coisas é a maior, a única coisa que não pode ser aprendida dos outros. Não sei se eu concordo com Aristóteles nisso. E um sinal da genialidade é transformar coisas, encontrar semelhanças entre coisas que não são semelhantes. O que nós queríamos verificar era esse tipo de coisa, esse fenômeno não local, com a minha filha, no aprendizado ou na memorização de tarefas. E fizemos isso e introduzimos lá também a expressão Homo metaforicus, que se refere ao fato de que o ser humano, aparentemente, é o único animal que faz metáforas. Porque tem animais que fazem ferramentas. Tem animais que se comunicam, e às vezes, melhor do que nós. Então, temos muitas coisas em comum com vários animais, várias espécies e nós. Mas a metáfora parece ser um privilégio da espécie humana.
Com essa febre que nós tivemos com relação ao negacionismo, essa descrença com relação à ciência, às instituições, tem muito a ver com redes sociais também, mas como jornalista, às vezes eu me preocupo um pouco do receio do cientista em usar metáforas para falar do seu trabalho, porque isso acabaria, segundo essa visão, depreciando todo o conceito científico, matemático, físico que há por trás disso. O senhor acha que os cientistas poderiam ficar menos ciosos em usar metáforas?
Eu acho que a metáfora, a boa metáfora, tem um valor universal, no sentido que o interlocutor capta imediatamente o que você quer dizer. Por isso que Aristóteles, na sua obra poética, a preza tanto. Então, eu acho que se alguém me pergunta o que é entropia, por exemplo, então eu avalio se o interlocutor quer uma resposta de 20 segundos, uma resposta de 5 minutos, uma resposta de horas ou uma resposta da vida toda. Na primeira abordagem, se você puder formular uma boa metáfora, você já comunicou para o outro um pouco do que que seja esse conceito. Aí, se o outro quer saber mais, você explica mais. Chega um momento que você diz, escuta, você não quer estudar física, física teórica? E nós continuaremos a nossa conversa em níveis cada vez mais detalhados, mais meticulosos, mas a conceituação terá sido transmitida, pelo menos um pouco, naquela primeira abordagem. A metáfora tem um valor imenso. Eu uso muito metáforas quando me fazem perguntas destinadas para o grande público. Depois, se quer saber mais, então vamos analisar mais.
Não sei se é verdade ou não, mas a queda da maçã que teria ajudado Newton a formular a Lei da Gravidade poderia ser também uma metáfora da entropia… Porque a maçã caiu, não tem como ela voltar, caiu de uma forma que, imprevisivelmente, não seria possível saber nem a trajetória…
Claro, a trajetória exata, não. A trajetória exata depende das condições iniciais exatas, que nunca saberemos quais foram. Se é verdade ou não que caiu uma maçã na cabeça de Newton. Porque numa das visitas que me convidaram em Cambridge, levaram-me na frente, acho que era do Trinity College, e tem uma árvore lá, uma macieira. E me falaram: dizem que essa foi a da maçã do Newton. Ninguém sabe. Mas as condições iniciais naquele momento não sabemos exatamente, nunca saberemos, e isso faz parte efetivamente do conceito de entropia. O conceito de energia é aquilo sobre o qual temos certezas. O conceito de entropia é aquilo sobre o qual temos incertezas. E a união dos dois conceitos, energia e entropia, é a base da termodinâmica.
(Colaborou Roger Marzochi)









