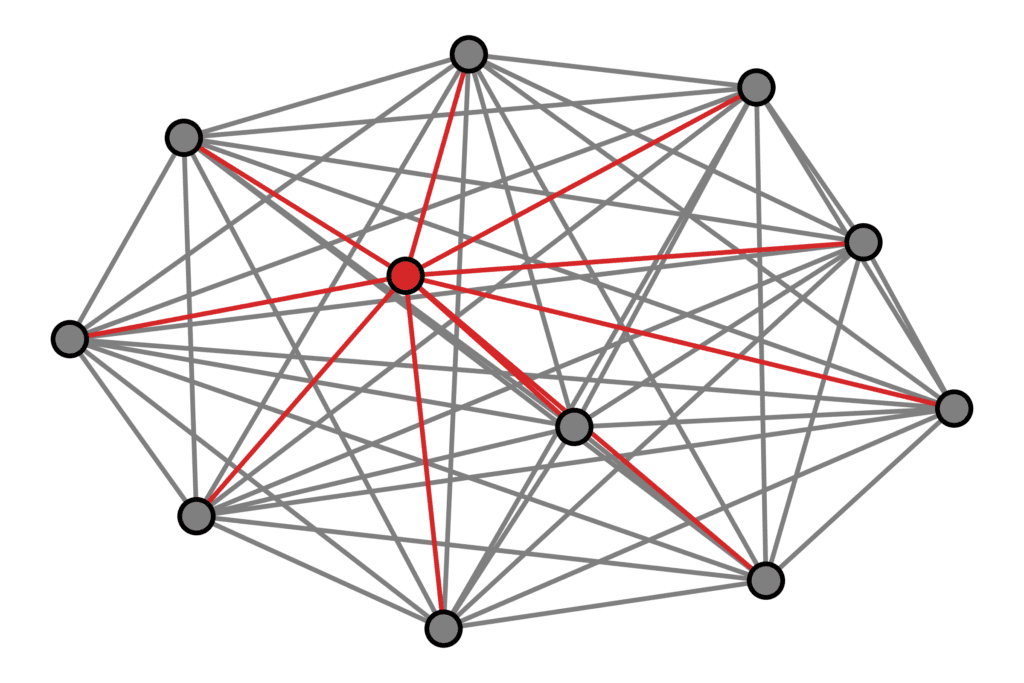
Crédito da Arte: Tobias Micklitz / Legenda: Imagem ilustra o nível (bolha vermelha) fracamente acoplado (linhas vermelhas) ao banho imperfeito (bolhas cinzas conectadas pelas linhas cinzas simbolizando quais estados do banho estão interagindo)
A análise estuda o decaimento de um estado fracamente acoplado a um “banho imperfeito”, ou seja, um conjunto finito de estados espalhados por níveis de energia discretos, e o surgimento da Regra de Ouro de Fermi quando o acoplamento ao banho aumenta
Conhecida como a Regra de Fermi de Transição, a Regra de Ouro de Fermi é um princípio fundamental na Física de sistemas quânticos formulado pelo físico italiano Enrico Fermi, um dos grandes cientistas do século XX. Essa regra descreve a taxa de transição entre estados quânticos iniciais e finais em sistemas que sofrem interações quânticas. Ela é aplicável em situações em que um estado quântico inicial está fracamente acoplado a um contínuo de outros estados finais que têm energias sobrepostas. Essa regra é uma forma de relatar a probabilidade de uma partícula em um estado quântico inicial fazer a transição para um estado quântico final.
Essa transição prevista nesta regra, que é amplamente utilizada em diversos campos da física, como física nuclear, física de partículas, teoria quântica de campos e mecânica quântica em geral, ocorre quando o estado inicial é acoplado a um “banho perfeito”, ou seja, um contínuo infinito de estados a decair. Um átomo excitado, por exemplo, pode decair e emitir um fóton, o qual pode viajar para qualquer direção. A Regra de Ouro de Fermi é perfeitamente aplicada nessas condições. Mas, e se o “banho” for imperfeito, ou seja, um sistema pequeno e isolado que tem níveis de energia discretos?
Essa foi uma das questões feitas pelo físico alemão Tobias Micklitz, do Centro Brasileiro de Pesquisas Físicas (CBPF), no artigo “Emergence of Fermi’s Golden Rule”, escrito por ele em companhia dos cientistas Alan Morningstar (Universidade de Princeton), Alexander Altland (Universität zu Köln) e David A. Huse (Instituto de Estudos Avançados, em Princeton) que foi publicado em setembro de 2022 na Physical Review Letters.
“Um limite extremo é quando o acoplamento é muito menor que a separação dos níveis do banho. Nesse caso a regra de Ouro de Fermi não se aplica, pois o sistema não possui estados finais para decair, e permanece em seu estado inicial. A gente estava interessado em como ocorre o crossover do Banho Perfeito para o outro caso”, explica Micklitz, que vive há dez anos no Brasil.
“A termalização em banhos imperfeitos é um tópico de bastante interesse e muito atual e o surgimento da Regra de Ouro de Fermi em banhos imperfeitos uma vez que o acoplamento aumenta, uma faceta do problema. No regime do crossover, encontramos uma dependência temporal bastante complexa na probabilidade de decaimento. Ou seja, uma dependência de tempo não monótona inesperada, com decaimento inicial, seguido por um aumento, antes de saturar a um valor constante. Podemos relacionar o perfil temporal à estatística dos níveis de energia do banho e à razão dos valores mínimos e de saturação da probabilidade à estatística de suas autofunções”, conclui Micklitz.
(Colaboração de Roger Marzochi)