Uma mesma equação matemática governando a dinâmica de um sistema físico pode dar origem tanto a um movimento caótico, praticamente imprevisível, quanto a outro estável, quase ou totalmente periódico. Tudo pode depender das condições iniciais, ou então dos valores dos parâmetros das equações do sistema. Em um trabalho publicado na revista Brazilian Journal of Physics, Paulo Rech, do Departamento de Física da Universidade do Estado de Santa Catarina (UDESC), analisa a dinâmica de um modelo matemático ecológico para o equilíbrio da população de duas espécies, uma presa e seu predador, convivendo em um certo habitat.
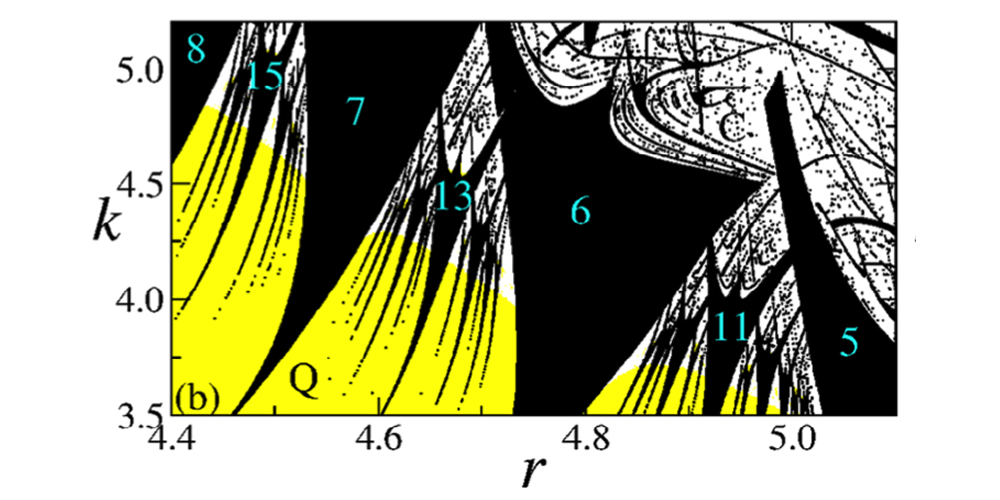
Comparando dois métodos diferentes de se realizar cálculos numéricos com o mesmo modelo, Rech identificou faixas de valores para dois parâmetros do modelo em que o sistema se comporta de maneira periódica (isto é, o ecossistema do modelo se encontra em equilíbrio, com as populações de presa e predador oscilando periodicamente). Essas faixas de periodicidade formam estruturas semelhantes às chamadas línguas de Arnold. Cada “língua” corresponde a uma região em que os parâmetros do sistema determinam uma dinâmica com período de número inteiro. Os gráficos obtidos na pesquisa mostram sequências dessas línguas, com os seus números inteiros seguindo diferentes padrões matemáticos. Comportamentos desse tipo já foram observados em sistemas físicos tais como lasers, circuitos eletrônicos e outros.
A pesquisa foi realizada com apoio financeiro do CNPq e da Fundação de Amparo à Pesquisa e Inovação do Estado de Santa Catarina (FAPESC).
Artigo Científico
On Two Discrete-Time Counterparts of a Continuous-Time Prey-Predator Model
Paulo C. Rech
Braz J Phys 50, 119–123 (2020)
Contato para imprensa
Igor Zolnerkevic
Assessor de comunicação
comunicacao@sbfisica.org.br