Em sua dinâmica turbulenta, o plasma confinado magneticamente em um tokamak sofre mudanças caóticas de trajetória que podem piorar ou melhorar o seu confinamento. Muita informação sobre esse transporte caótico de grupos de trajetórias de uma região do espaço de fase para outra pode ser obtida analisando sistemas dinâmicos mais simples, como os mapeamentos bidimensionais que preservam áreas, os mapas simpléticos.
Em um artigo do Brazilian Journal of Physics, Ricardo Viana, da Universdidade Federal do Paraná (UFPR) e seus colegas, fazem uma revisão de resultados recentes sobre barreiras de transporte em mapas simpléticos, se concentrando em sistemas que não obedecem a chamada propriedade de torção.
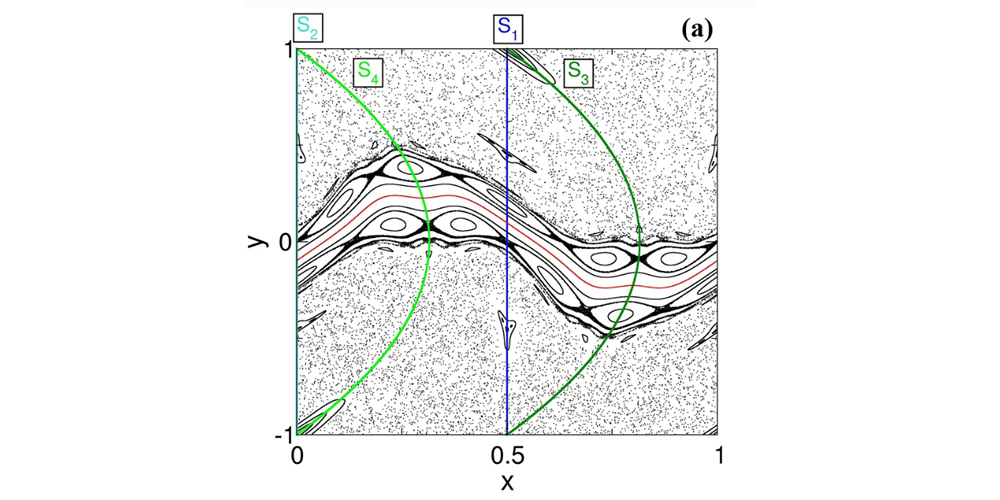
Em geral, os mapas simpléticos podem ser analisados utilizando a teoria resultante do teorema de Komolgorov-Arnold-Moser (KAM). Entretanto, em sistemas que não obedecem a chamada propriedade de torção, a teoria KAM padrão não vale em toda parte e surgem novas características dinâmicas: a reconexão não-resistiva, as curvas e bifurcações sem cisalhamento. Após apresentarem algumas propriedades gerais de um mapeamento sem torção padrão, Viana e seus colegas consideram mapeamentos das linhas de campo magnético para plasmas confinados magneticamente em tokamaks.
A pesquisa foi realizada com apoio financeiro da FAPESP, CAPESP e CNPq
Artigo Científico
Transport Barriers in Symplectic Maps
L. Viana, I. L. Caldas, J. D. Szezech Jr., A. M. Batista, C. V. Abud, A. B. Schelin, M. Mugnaine, M. S. Santos, B. B. Leal, B. Bartoloni, A. C. Mathias, J. V. Gomes e P. J. Morrison
Braz J Phys 51, 899–909 (2021)
Contato para imprensa
Igor Zolnerkevic
Assessor de comunicação
comunicacao@sbfisica.org.br