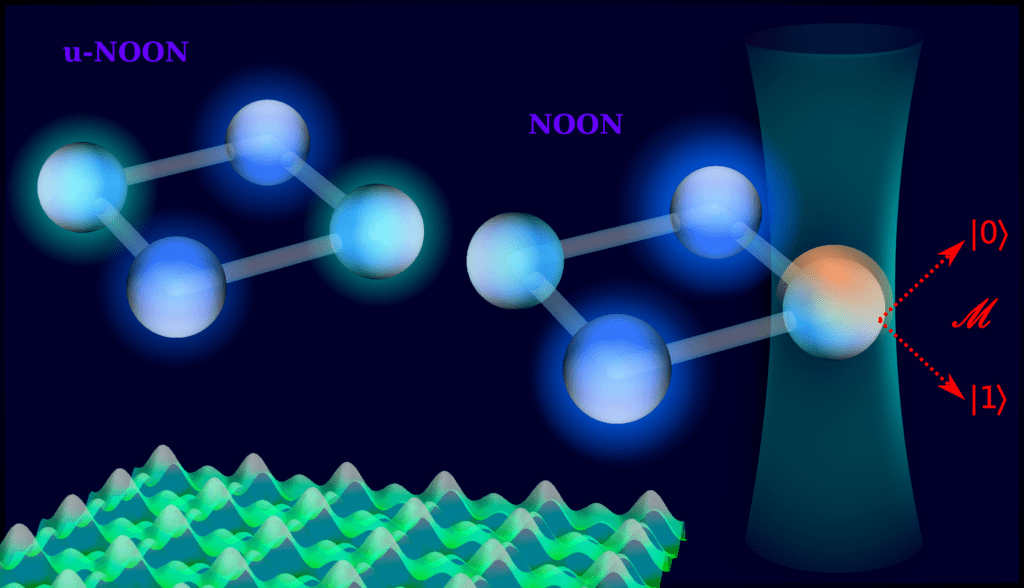
Integrabilidade em matemática refere-se a equações com características especiais que permitem uma compreensão profunda de suas propriedades. No trabalho “Integrable Atomtronic Interferometry”, mostramos como utilizar a integrabilidade para gerar e controlar, com alta precisão e fidelidade, um determinado estado quântico, da classe dos estados do tipo “gato de Schrödinger”, conhecido como “estado NOON”. É um estado emaranhado que surge como forte candidato para diversas aplicações nas áreas de computação, comunicação, metrologia e sensoriamento quânticos. Sua aplicação deve estender-se também para áreas como a química e a biologia.
A arquitetura para implementação deste programa é através de sistemas atômicos ultrafrios, onde os átomos são resfriados e presos em armadilhas ópticas a temperaturas próximas ao zero absoluto. Nesse ambiente, o comportamento ondulatório dos átomos é evidenciado. A partir desta estrutura, projetamos um sistema que opera como um interferômetro e produtor de estados NOON.
Um diferencial deste resultado é que o tempo previsto para gerar estados NOON é independente do número total de partículas, oferecendo uma perspectiva encorajadora de escalabilidade. O trabalho ilustra o potencial da integrabilidade no aprimoramento de tecnologias quânticas emergentes.
Este trabalho faz parte da tese de doutorado de Karin Wittmann Wilsmann, supervisionado pela Profa. Angela Foerster, ambas do Instituto de Física da UFRGS. Contou também com a colaboração do aluno Daniel Grün (UFRGS), dos Profs. Leandro Ymai e Arlei Tonel da UNIPAMPA, Bagé, e do Prof. Jon Links da Universidade de Queenslad, Austrália.
Artigo científico:
Integrable Atomtronic Interferometry,
D. Grün, L. Ymai, K. Wittmann, A. Tonel, A. Foerster, and J. Links,
Phys. Rev. Lett., 129, 020401 (2022), DOI: 10.1103/PhysRevLett.129.020401
Artigo científico relacionado:
Protocol designs for NOON states,
Daniel S. Grun, Karin Wittmann W., Leandro H. Ymai, Jon Links, and Angela Foerster.
Comm. Phys., 5, 36 (2022), DOI: 10.1038/s42005-022-00812-7
Note: The first three authors contributed equally. The names are in alphabetical order!