Uma grande biodiversidade aumenta as chances de sobrevivência de um ecossistema. Uma produção mais diversificada tende a tornar um país mais resiliente a crises econômicas. Muitos campos da ciência apresentam situações assim, em que um recurso finito precisa ser dividido, e a diversidade na divisão parece essencial. Um novo estudo de físicos brasileiros e italianos sugere uma relação entre a maximização da diversidade em sistemas complexos e a lei de Zipf.
A equipe de Jeferson Arenzon, professor da Universidade Federal do Rio Grande do Sul (UFRGS) e membro do INCT de Sistemas Complexos, analisou o problema geral da fragmentação de um sistema de tamanho S em pedaços inteiros que obedece a lei de Zipf. “Os fragmentos podem ser as cidades de um país com S habitantes ou as diferentes palavras que aparecem um certo número de vezes em um livro de S palavras no total”, Arenzon explica no vídeo. “No caso dos livros, o número de vezes que cada palavra aparece é inversamente proporcional a sua posição no ranking de frequência.”
O trabalho publicado em setembro na Physical Review Letters foi uma colaboração entre os pesquisadores Amanda de Azevedo Lopes, doutorada pela UFRGS sob orientação de Arenzon, e Onofrio Mazzarisi, doutorado orientado por Federico Corberi, na Universidade de Salerno, na Itália. Eles usaram um modelo estatístico simples para analisar a fragmentação e a diversidade dos tamanhos desses fragmentos.
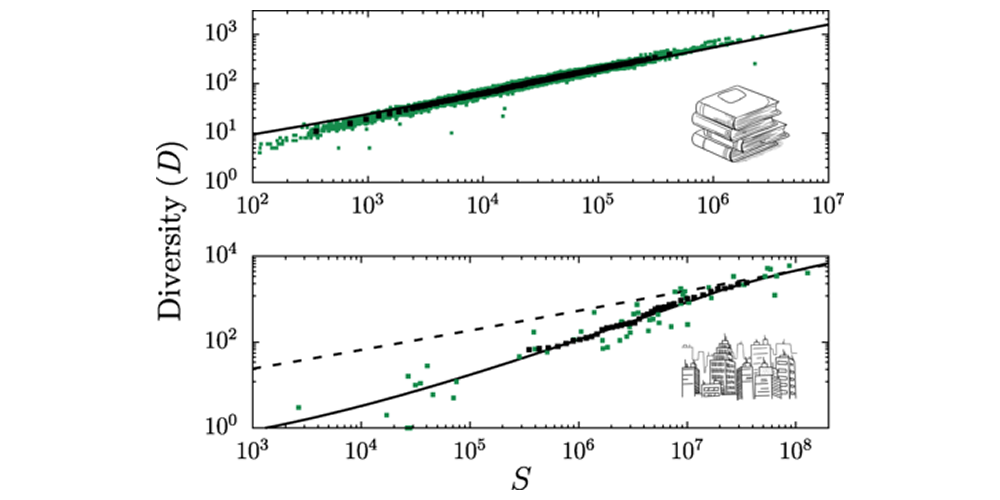
O modelo assume que a distribuição do número de diferentes tamanhos dos fragmentos segue uma lei de potência geral e mede a diversidade do sistema pelo número de diferentes tamanhos desses fragmentos. Os físicos compararam as previsões do modelo com os dados de dois tipos de sistemas reais: o tamanho das populações de todas as cidades da Europa e a frequência das palavras de mais de 30 mil livros do Projeto Gutenberg.
Os resultados mostraram que a lei de potência que melhor descreve os dados é a que maximiza a diversidade dos fragmentos. E essa lei de potência é exatamente a lei de Zipf.
“O fato da lei de Zipf aparecer ao mesmo tempo em que a diversidade atinge um máximo parece ser uma propriedade geral desse sistemas, independente do mecanismo específico que gera a lei de Zipf”, conclui Arenzon. “Temos agora uma nova perspectiva para analisar esses sistemas complexos.”
O estudo foi realizado com financiamento da CAPES e do CNPq.
Artigo científico
Maximal Diversity and Zipf’s Law
Onofrio Mazzarisi, Amanda de Azevedo-Lopes, Jeferson J. Arenzon e Federico Corberi
Phys. Rev. Lett. 127, 128301 – 16 de setembro de 2021
Contato para imprensa
Igor Zolnerkevic
Assessor de comunicação
comunicacao@sbfisica.org.br