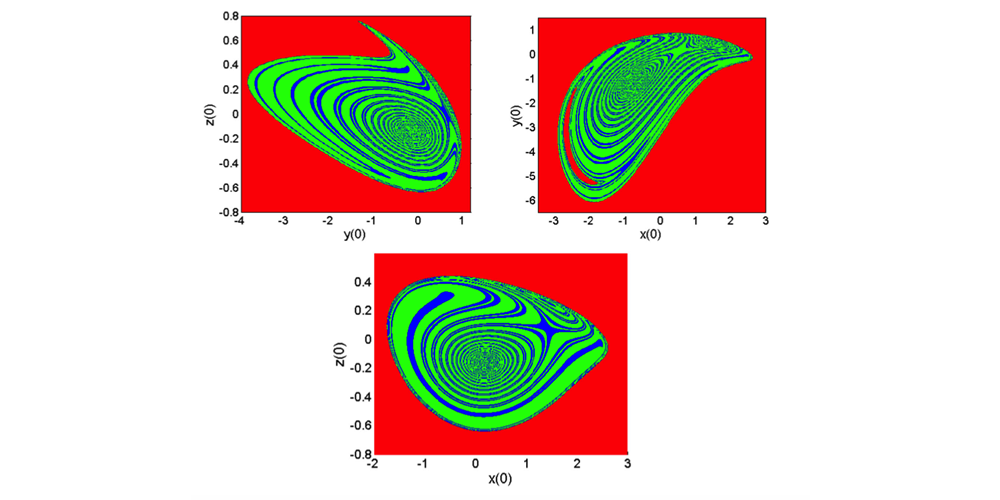
Jacques Kengne e seus colegas da Universidade de Dschang, Camarões, em colaboração com pesquisadores da Universidade de Tecnologia de Golpayegan e da Universidade de Tecnologia Amirkabir, ambas no Irã, investigaram as propriedades dinâmicas de um novo sistema de equações diferenciais em três dimensões. Eles identificaram no espaço de fase do sistema o que a literatura recente chama de atrator oculto: uma bacia de atração, ou região de estabilidade no espaço de fase que não possui intersecção com nenhum ponto de equilíbrio, sendo portanto mais difícil de ser identificada matematicamente. Entender os atratores caóticos pode ser útil em aplicações em engenharia, uma vez que podem produzir respostas inesperadas e potencialmente desastrosas a perturbações em sistemas tais como uma ponte ou as asas de um avião.
No trabalho publicado na edição de agosto do Brazilian Journal of Physics, Kengne e seus colaboradores realizam uma análise teórica do sistema, bem como apresentaram simulações numéricas de um circuito eletrônico cuja dinâmica é governada pelas mesmas equações. Concluem que o sistema analisado é um exemplo de uma classe de sistemas não-lineares recém descoberta e restrita, a dos sistemas que desenvolvem caos não-hiperbólico. Sistemas caóticos são sistemas cuja dinâmica pode mudar drasticamente mesmo com pequenas modificações nas condições iniciais. Diferente dos hiperbólicos, o equilíbrio de sistemas não-hiperbólicos nunca pode ser garantido, sendo estruturalmente instáveis.
Artigo Científico
Chaos and Coexisting Bifurcations in a Novel 3D Autonomous System with a Non-Hyperbolic Fixed Point: Theoretical Analysis and Electronic Circuit Implementation
J. Kengne, H. Abdolmohammadi, V. Folifack Signing, S. Jafari e G. H. Kom
Braz J Phys 50, 442–453 (2020)
Contato para imprensa
Igor Zolnerkevic
Assessor de comunicação
comunicacao@sbfisica.org.br