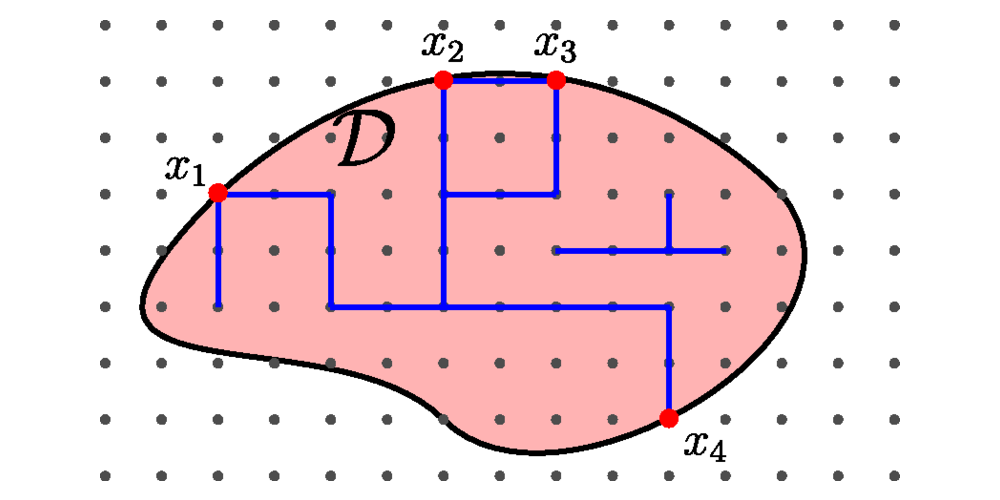
O estudo de teorias de campo conformes tem uma variada gama de aplicações na física, algumas já conhecidas e outras que ainda estão a ser mapeadas.
Sabemos que o estudo de simetria conforme em duas dimensões já se mostrou útil para o estudo de modelos de mecânica estatística clássicos desde a década de 1980, além de ter encontrado aplicações importantes em estudos quânticos, envolvendo fenômenos como o efeito Hall quântico e emaranhamento.
Um novo trabalho por uma dupla de físicos italianos, Giacomo GOri, do SISSA, em Trieste, e Jacopo Viti, do Instituto Internacional de Física da UFRN (Universidade Federal do Rio Grande do Norte), em Natal, faz uma exploração inédita desse campo de estudo, ao apresentar uma fórmula exata para descrever um modelo crítico bidimensional conhecido como modelo de Ising.
“Neste artigo, pela primeira vez, calculamos exatamente uma função de correlação com uma singularidade logarítmica no modelo de Ising em duas dimensões”, diz Viti.
“O artigo é importante por duas razões: a primeira é que ele mostra uma aplicação concreta da teoria conforme logarítmica no modelo de mecânica estatística extremamente importante e clássico, o modelo de Ising em duas dimensões. E a segunda razão é que confirma a necessidade de estender a teoria conforme clássica, que descreve os problemas tradicionais de mecânica estatística no ponto crítico, para incluir também funções de correlações com singularidade logarítmica.”
O trabalho foi publicado em 6 de novembro no “Physical Review Letters”.
Para ler o artigo completo, clique aqui (só para assinantes) ou aqui (acesso livre).