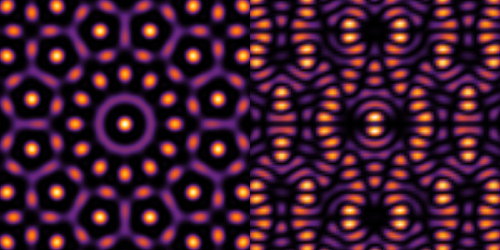
Um novo trabalho teórico com participação brasileira ajuda a esclarecer os critérios e classificação de transições de fase quânticas em sistemas desordenados. É proposta uma classificação unificada para as transições na presença de desordem fraca através da análise pelo critério de Harris e o comportamento das chamadas singularidades de Griffiths.
Na física clássica, transições de fase fazem parte do nosso cotidiano. Quando a água de uma poça evapora, estamos vendo uma transição da fase líquida para a gasosa. Para compreender exatamente como isso se dá, no entanto, é preciso mergulhar no mundo microscópico, onde o comportamento das partículas individuais que compõem todos os materiais é regido em última análise pela Mecânica Quântica.
Uma das formas de estudar esses processos é por meio da mecânica estatística, que analisa os processos estocásticos que produzem conjuntamente o comportamento do sistema .
Esse é um dos instrumentos utilizados no artigo de Thomas Vojta, da Universidade de Ciência e Tecnologia do Missouri, nos Estados Unidos, com José A. Hoyos, do Instituto de Física de São Carlos da Universidade de São Paulo, publicado na “Physical Review Letters”.
Ele estabelece uma relação entre singularidades de Griffiths, que ocorrem em sistemas desordenados de mecânica estatística, e o critério de Harris, que sugere que a variação da média de temperatura pseudo-crítica em um dado volume precisa ser menor que sua diferença da temperatura crítica global, para manter a classe de universalidade das transições de fase quânticas.
“Se um ponto crítico limpo viola o critério de Harris, ele é desestabilizado por desordem fraca”, escrevem os dois autores. “Ao mesmo tempo, o expoente dinâmico de Griffiths z’ diverge ao se aproximar da transição, sugerindo comportamento crítico não-convencional.”
Segundo os pesquisadores, esse trabalho teórico pode ser aplicado a uma variedade de sistemas, que vão de correntes de spin quântico, sistemas clássicos de reação-difusão e ímãs metálicos. Na prática, a dupla propõe que é possível fazer uma classificação unificada de transições de fase em sistemas desordenados com base nesses alicerces.
Para ler o trabalho completo clique aqui (para assinantes) ou aqui (acesso livre).