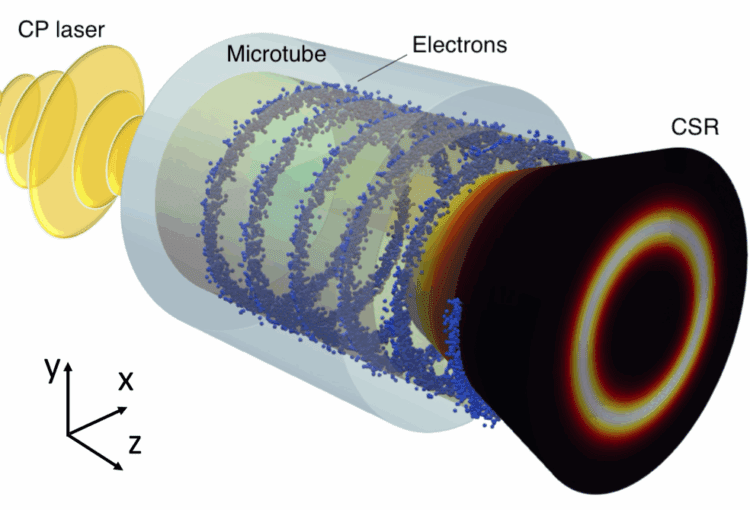
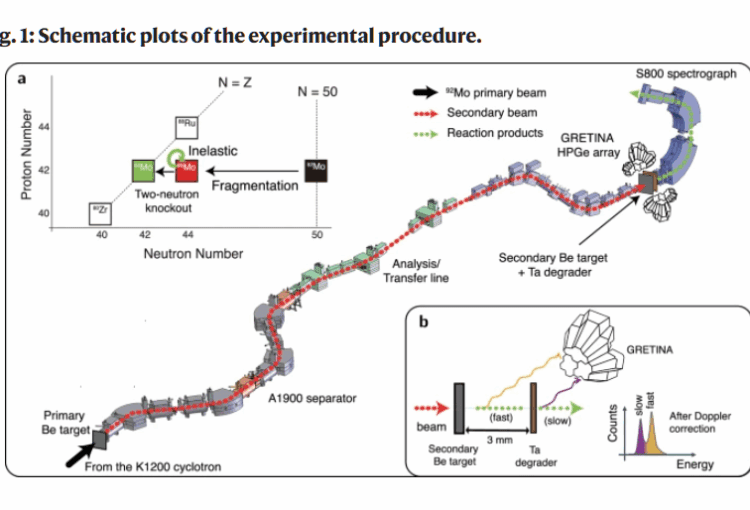
Em mecânica estatística, grafos dirigidos permitem representar as relações entre os graus de liberdade de um sistema dinâmico, como redes neurais, redes de transporte e mesmo a internet.
A dinâmica de sistemas complexos governados pelos grafos dirigidos, por sua vez, pode ser estudada pelas chamadas matrizes não-Hermitianas aleatórias, e é sobre elas que se debruça um novo estudo com participação brasileira.
Em artigo publicado no “Physical Review Letters” em 23 de novembro, Izaak Neri, do Instituto Max Planck para Física de Sistemas Complexos, na Alemanha, e Fernando Lucas Metz, do Departamento de Física da Universidade Federal de Santa Maria (RS), apresentam uma teoria geral e exata para explicar os valores aberrantes que surgem nos espectros das matrizes não-Hermitianas aleatórias, lançando mão de uma estrutura de árvore local.
“Nós mostramos que esses observáveis espectrais obedecem a expressões universais, que se mantêm para uma ampla classe de matrizes aleatórias orientadas”, escrevem os pesquisadores.
Para ler o artigo completo, clique aqui (só para assinantes) ou aqui (acesso livre).