O estudo de redes tem uma gama de aplicações que impressiona: as mesmas estratégias podem permitir a investigação do fluxo de saída de pessoas num estádio de futebol, as conexões entre neurônios no cérebro e a transmissão da dados via internet, para citar apenas três exemplos.
Agora, um grupo de pesquisadores do Brasil e da Europa usou as ferramentas matemáticas das redes para estudar epidemiologia, ao formular como uma doença pode se espalhar em uma população em termos das redes de contágio que as pessoas formam entre si.
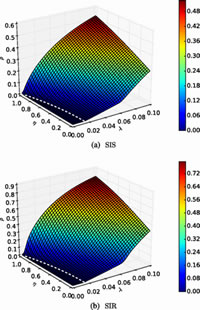
“Usando o método de estado quasi-estacionário, nós mostramos numericamente a existência de localização da doença e a emergência de dois ou mais picos de suscetibilidade, que são caracterizados analiticamente e numericamente pela taxa inversa de participação”, escrevem os autores em artigo publicado em 2 de fevereiro na “Physical Review X”.
Para criar o modelo, os pesquisadores lançam mão de tensores, objetos matemáticos que permitem a representação de dados multidimensionais de uma forma compacta. “Por análises matemáticas e simulações numéricas, encontramos várias características interessantes como a existência de múltiplos limites epidêmicos e taxas de transmissão além das quais o número de indivíduos que pegam uma doença é não negligenciável”, dizem.
O trabalho foi realizado por Guilherme Ferraz de Arruda e Francisco A. Rodrigues, do Instituto de Ciências Matemáticas e de Computação da Universidade de São Paulo em São Carlos (SP), Emanuele Cozzo e Yamir Moreno, da Universidade de Zaragoza, na Espanha, e Tiago P. Peixoto, da Universidade de Bath, no Reino Unido.
Para ler o artigo completo, clique aqui (só para assinantes) ou aqui (acesso livre).
Assessoria de comunicação da SBF
Salvador Nogueira
Tel: +55 11 99178-9661
E-mail: comunicacao@sbfisica.org.br
Twitter: http://twitter.com/sbfisica
Facebook: http://www.facebook.com/sbfisica