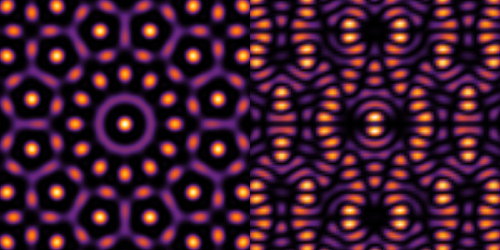
O teorema de Bloch é de importância fundamental para a física da matéria condensada, pois permite representar de forma simplificada e conveniente as funções de onda para uma partícula em um potencial periódico, típico de estruturas cristalinas, em termos das chamadas ondas de Bloch.
Agora, uma dupla de pesquisadores do Instituto de Física de São Carlos da Universidade de São Paulo propõe a utilização desse mesmo método no estudo numérico de um problema bem diferente: a descrição de correlações de campos de glúons na cromodinâmica quântica (QCD), através da formulação de rede da teoria.
De acordo com os autores, Tereza Mendes e Attilio Cucchieri, tais correlações seriam calculadas para configurações de campos de glúons geradas em simulações de Monte Carlo, e o conhecimento detalhado de seu comportamento no limite infravermelho pode contribuir para explicar o fenômeno de confinamento de cor na QCD. “Porém, para que seja atingido esse limite, que corresponde a baixas energias ou grandes distâncias, as redes usadas nas simulações devem ser suficientemente grandes”, explica Mendes.
O método, descrito em artigo publicado em 9 de maio no periódico “Physical Reviews Letters” e destacado como “Sugestão do Editor”, oferece um avanço importante, ao permitir que o estudo seja feito em redes muito menores do que as usuais, com a obtenção dos mesmos resultados físicos, ou, inversamente, que os resultados obtidos sejam válidos para redes muito maiores do que as usadas na simulação.
“O ganho é alcançado porque as duas etapas do estudo numérico – a geração de campos gluônicos (ou termalização) e a fixação de gauge para esses campos – são tratadas diversamente, utilizando-se duas escalas distintas de distâncias”, esclarece a co-autora do trabalho.
“Mais precisamente, considera-se a termalização em uma rede pequena, que será replicada N vezes, fornecendo o análogo de um potencial periódico para o passo da fixação de gauge dos campos. Esse passo, que corresponderia a um cálculo na rede grande, é então realizado empregando-se o teorema de Bloch, o que significa que o problema será estudado efetivamente apenas na rede inicial, pequena, reduzindo significativamente o custo computacional da simulação.”
Para ler o artigo completo, clique aqui (só para assinantes) ou aqui (acesso livre).
Assessoria de comunicação da SBF
Salvador Nogueira
Tel: +55 11 98481-6119
E-mail: comunicacao@sbfisica.org.br
Twitter: http://twitter.com/sbfisica
Facebook: http://www.facebook.com/sbfisica