Pode o bater de asas de uma borboleta sobre o campus da UNESP em Rio Claro desencadear uma tempestade? A metáfora do “Efeito Borboleta”, popularizada em 1961 pelo meteorologista Edward Lorenz, nos ensina sobre a sensibilidade e o impacto de pequenas variações em sistemas complexos. Agora, no próprio campus da Universidade Estadual Paulista, essa metáfora ganha vida através de uma descoberta que promete abalar as fundações da física e da matemática.
Recentemente, os pesquisadores Vinícius de Barros da Silva, doutor em Física Aplicada pela UNESP, juntamente com seus orientadores Edson Denis Leonel e o matemático João Peres Vieira, solucionaram a segunda parte do 16º problema de Hilbert. Esse desafio, lançado em 1900 pelo matemático alemão David Hilbert, intrigou matemáticos com sua complexidade e resistiu a todas as tentativas de solução. A resolução foi publicada em 30 de agosto de 2024 no artigo “Exploring Limit Cycles of Differential Equations through Information Geometry Unveils the Solution to Hilbert’s 16th Problem”, na revista científica Entropy.
De acordo com a matéria do Jornal da UNESP, escrita pela jornalista Malena Stariolo, o 16º problema de Hilbert, que estuda a topologia de curvas e superfícies algébricas, buscava uma resposta sobre o número máximo e as posições de “ciclos limites” em sistemas dinâmicos. Esses ciclos são padrões de repetição ao longo do tempo, visíveis em fenômenos naturais e artificiais, como o funcionamento de sistemas de refrigeração: à medida que a temperatura aumenta, o sistema é ativado e, ao atingir certo limite, é desligado, reiniciando o ciclo.
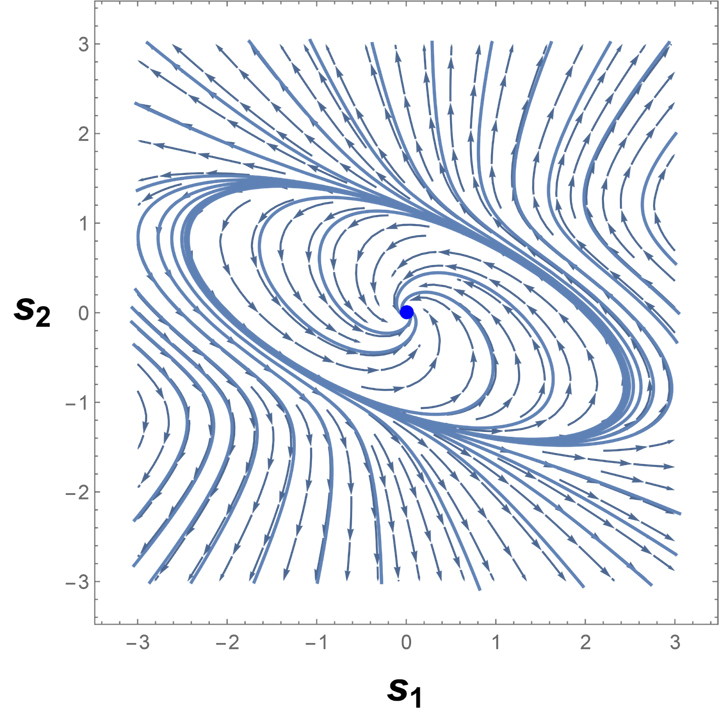
Para responder ao problema, os pesquisadores da UNESP desenvolveram a “Teoria Geométrica de Bifurcações” (TGB), que combina geometria informacional e mecânica estatística. “Esse desenvolvimento nasceu de uma ideia matemática do Vinícius, que pavimentou uma rota que não existia para a solução do problema de Hilbert. Há mais de 100 anos, cientistas de todos os continentes tentaram resolver esse problema sem êxito. A geometria de informação trouxe uma nova abordagem que se mostrou crucial. Diferentemente das abordagens tradicionais, que dependiam de métodos perturbativos, a TGB utiliza a curvatura escalar para revelar os ciclos limites”, explica Leonel, em entrevista ao Boletim SBF.
Vinícius conseguiu encontrar as respostas ao problema a partir da mecânica estatística e de estudos da geometria informacional de Fisher, que leva o nome do pesquisador Sir Ronald A. Fisher, estatístico britânico e biólogo evolutivo, considerado como um dos fundadores da estatística moderna, que cria mapas cuja geometria mede a “curvatura” ou a variação em um espaço de informações, essencial para previsão em sistemas dinâmicos e na modelagem de incertezas. A partir desses cálculos, Vinícius criou a TGB.
De acordo com Vinícius, “nós vimos que existe um paralelo muito grande entre a física estatística e a dinâmica não linear”. “A geometria de informação nasce da física estatística e já vinha sendo usada nesse contexto para explorar os mais variados fenômenos. Só que nós percebemos que ela tinha um potencial gigantesco para ser aplicada em sistemas dinâmicos. Foi aí que surgiu a TGB, que é uma nova maneira de investigar sistemas dinâmicos ou complexos, usando a geometria de informação que, por sua vez, envolve o estudo de métricas riemannianas e a curvatura escalar”, explica o jovem cientista ao Boletim SBF.
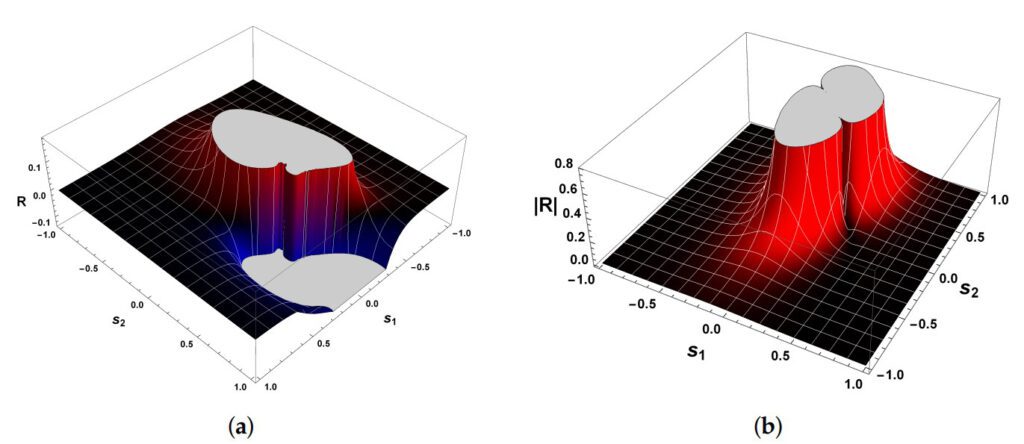
“Essa métrica induz sobre o espaço uma curvatura chamada de curvatura Escalar. E é essa curvatura que releva os segredos por trás de sistemas dinâmicos de uma forma muito direta, analítica e sem a necessidade de métodos perturbativos ou teoremas negativos que, por sua vez, não permitiam abordar o problema de Hilbert na sua concepção original. Esse foi o grande diferencial da nossa abordagem”, afirma o pesquisador.
O rigor matemático da pesquisa foi reforçado pelo experiente matemático João Peres Vieira, que ajudou a validar a solução. “O Vinícius chegou em minha sala e disse que havia encontrado a resposta para o problema. Mas, a gente precisa dar um rigor matemático para isso. Essa foi a minha contribuição: ajudar o Vinícius a fazer uma prova rigorosa e comprovar a exatidão do resultado”, afirma Vieira, também em entrevista ao Boletim SBF.
Além de melhorar a previsão climática, essa teoria inovadora abre caminho para pesquisas em saúde, computação e áreas que exploram sistemas dinâmicos. Para os pesquisadores, a abordagem oferece uma nova maneira de entender padrões que regem fenômenos naturais e artificiais.
Comprometido com a sustentabilidade e a inovação, o campus da UNESP em Rio Claro investiu recentemente em energia solar, refletindo sua missão científica. Assim como o “efeito borboleta” sugere, talvez a matemática nascida aqui em Rio Claro reverbere globalmente, trazendo previsões mais certeiras e avanços que impactem o mundo.
(Colaborou Roger Marzochi)








