Após estudar alguns papers, jovem cientista desenvolve algoritmo que somente um ano depois viria a ser descoberto como o mais rápido já feito
Santiago Giménez de Castro tem 31 anos e uma trajetória acadêmica muito profícua. Graduou-se em Física pela Universidade de São Paulo (USP), em 2015, tornou-se mestre em Engenharia Espacial pelo Instituto Nacional de Pesquisas Espaciais (Inpe), em 2019, e se fez Doutor em Engenharia Elétrica na área de fotônica na Universidade Presbiteriana Mackenzie, em 2023. E foi na área de computação no Mackenzie que ele obteve grande destaque, ao descobrir, meio que por acaso e intuição, um algoritmo para se calcular a condutividade de nanomateriais de forma muito mais rápida que o método tradicional.
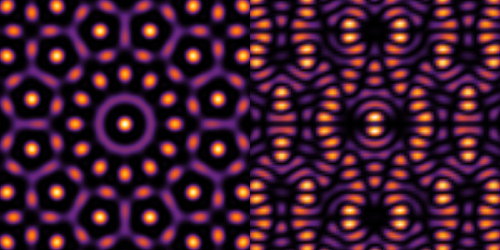
Ele detalha esse achado no artigo “Fast Fourier-Chebyshev Approach to Real-Space Simulations of the Kubo Formula”, publicado dia 16 de fevereiro de 2024 no periódico Physical Review Letters (PRL). “Sinceramente, foi muito estranho o que ocorreu. Eu desenvolvi esse algoritmo nas primeiras semanas que trabalhei com esses métodos. Mas eu não sabia comparar o desempenho dos diferentes métodos ainda. Também não conhecia todas as abordagens utilizadas, e não tinha como saber se não havia alguma mais eficiente. Um ano depois, fui passar um período de 12 meses na York University (Inglaterra) e, depois de amadurecer bastante no meu conhecimento da área graças aos meus orientadores, eu entendi o que havia feito”, explica o cientista, que iniciou o ano em Barcelona, na Espanha, onde começará o seu pós-doutorado no Instituto Catalão de Nanociência e Nanotecnologia (ICN2).

“Eu misturei dois papers diferentes e saiu esse método. Eu não entendia bem os papers porque achava que aquela deveria ser a forma que o algoritmo tinha que ser implementado. Não percebia que aquilo na verdade era uma novidade superimportante e acabou sendo uma contribuição legal”, explica em entrevista ao Boletim da Sociedade Brasileira de Física (SBF).
Para se calcular com o KPM a condutividade de um nanomaterial, como o grafeno, por exemplo, cada átomo é representado como um elemento da diagonal de uma matriz, chamada de Hamiltoniano. Assim, o Hamiltoniano é uma matrix de D linhas por D colunas. Em um pequeno material, há milhões de átomos. O método utilizado até então para se chegar à condutividade é o Kernel Polynomial Method (KPM). Este método utiliza a matriz hamiltoniana a partir da qual serão construídas duas sequências de vetores, a partir do número de átomos (D) e “M” vetores. Por esse método tradicional, a condutividade é calculada a partir da multiplicação dessas duas matrizes.
Nesta área, as propriedades de um nanodispositivo são obtidas a partir da chamada matrix Hamiltoniana do sistema. Os modelos que utilizamos representam cada átomo do dispositivo como um elemento da diagonal desta matriz. Sendo assim, o Hamiltoniano é uma matriz DxD, onde D é o número de átomos. Para avaliar a condutividade do dispositivo, o Kernel Polynomial Method (KPM) constrói duas outras matrizes, D x M em tamanho, onde M é um parâmetro que controla a resolução. A condutividade obtida a partir da multiplicação entre estas duas matrizes.
“Mas elas são ainda muito grandes. Mesmo um pequeno dispositivo há milhões de átomos, sendo assim D está na ordem do milhão e as matrizes do KPM podem chegar a ocupar dezenas de terabytes. A multiplicação entre elas pode demorar uma infinidade para ser feita. O que eu descobri é que dá para evitar esse passo”, diz Giménez de Castro. A partir de suas descobertas no início da pesquisa, o cientista buscou usar uma abordagem fundamentada em uma Transformada Rápida de Fourier (FFT), na qual não é necessário multiplicar as duas matrizes, mas apenas realizar FFTs em cada uma de suas linhas.
“E isso tem um custo enormemente reduzido. Para fazer a multiplicação entre matrizes precisa D x M2 operações. E para fazer as FFT são necessárias apenas D x M log M operações. Como M varia entre mil a 100 mil, você vê quanto mais rápido é a FFT: algo na ordem de 10 a mil vezes mais rápido. Quanto maior o M, mais rápido é o meu método em comparação à abordagem tradicional. A diferença entre os dois aumenta na medida que o M aumenta”, explica o cientista.
Agora, com seu pós-doutorado no ICN2, ele aposta em novas contribuições para desvendar a natureza de algoritmos. “Digamos que apesar de ser físico, a principal contribuição que dei foi em algoritmos e métodos computacionais, uma física matemática. E no ICN2 o pessoal faz a mesma coisa, métodos computacionais para a física.”
(Colaborou Roger Marzochi)